4.7 ★★★★☆  on Google


Products Icon  PRODUCTS


☰  All Products

  1. Log learning set
  2. LAS file Editor
  3. Alias Editor
  4. LAS log Displayer
  5. Functions Workflow
  6. Muti-well Work-flow
  7. Summaries & Upsc
  8. Ionic Water Analysis

  9. Well Log Scripting:

Services Icon  CONSULTING


☰  All Services

  1. Assembling
  2. Processing
  3. Interpretation

Training Icon  TRAINING

Youtube video 20 px icon  VIDEOS


☰  All Videos

  1. How to plot a LAS file
  2. Export data to Excel
  3. The log-plot display
  4. Flatten MD to TVDSS
  5. Function Workflows
  6. Petrophysical Aliases
  7. Multiwell Workflows
  8. Summaries & Upsc.
  9. Water Salinity
  10. Mineral Solvers
  11. Multizone Parameters

HandBook Icon  RECIPES

☰  All Recipes

  1. Merging LAS files
  2. Depth curve shifting
  3. Points interpolation
  4. Curves calibration
  5. Confidence bands
  6. Build Permeab. Corr.
  7. Demo files data set
  8. Core Data Import
  9. Computing Net-Pay
  10. Petrophysical Cutoffs
  11. VSH from GR index
  12. VSH from Neut-Dens
  13. Water Saturations
  14. Indonesia Water Sat.
  15. Mod. Simandoux Eq
  16. Fracture Porosity
  17. Geomechanic Logs
  18. Split Rock Volume
  19. Mineral Solvers
  20. Pay Indicator Index
  21. Water Salinity & Rw
  22. Estimating RHOM
  23. Estimating Rw & m

Paper Icon  PAPERS

  1. SWirr from well logs
  2. Water Sat. from Rxo
  3. Porosity from Rxo
  4. Porosity from Rt
  5. Vshale or Vclay ?
  6. Gas cap detection
  7. Biased Beta Distr
  8. Shaly Pickett Plot Eq.

Reference Flag Icon REFERENCE

Team icon  GET IN TOUCH


Home link icon
Download Icon Downloads PriceTag Icon Prices Youtube video 20 px icon Videos
CD Product Icon Products
Services Icon Consulting
Learn Icon Training
Team Icon About
Contact Icon Contact
4.7 ★ on Google Consulting Training      More ☰

$3,880 Life time license  (Reg.: $9,880)

Offer expires on April 30, 2024.
Full perennial license + auto-updates
+ 1 license migration + learn set

GeolOil offer expires soon
Genuine stand-alone, non-cloud license!


GeolOil - The Modified Simandoux Equation for Water Saturation


The Modified Simandoux Equation is an extension of the equation for shaly rocks to cover the cases where the saturation exponent n ≠ 2. The Simandoux equation of 1963 was one of the first models to successfully incorporate and correct the excess of conductivity in the matrix due to the presence of dispersed clays (the Archie equation of 1942 over-estimates amount of water saturation if there are clays). In its common standard version by Bardon and Pied (1969), the equation is:


Modified Simandox Equation for Water Saturation, Bardon and Pied (1969)


notice that if n=2, the equation takes the form of a second degree polynomial a.x2 + b.x + c = 0 on x=SW, which solution is the regular Simandoux equation. Also, the porosity to be used in the model, is the effective porosity φe corrected for shale content, not the total porosity φT.


When n≠2, the modified Simandoux equation can be solved by recursive numerical iterations. Start with an approximate guessed solution for SW, like the value found from the regular Simandoux equation, and keep iterating until convergence is reached within a desired numerical difference precision between SW and SWguess (usually 3-5 iterations are enough):


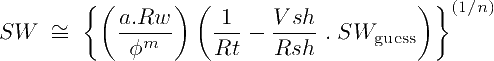
Solving the Modified Simandox Equation by numerical iterations



light bulb idea PROOF OF THE SIMANDOUX EQUATION:


Both the modified Simandoux equation (n≠2), and its regular version (n=2) can be deduced from the Archie equation rewritten in terms of true far field deep conductivity (1/Rt, the inverse of resistivity):

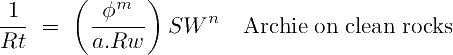
Archie Saturation Equation in terms of Conductivity


If the rock is shaly (Vsh ≥0), the deep conductivity (1/Rt) must be higher than the Archie conductivity because the clays transmit some electricity:

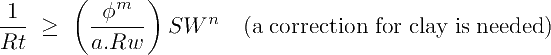
Deep conductivity must be higher than Archie conductivity in the presence of clays


The excess on conductivity can be adjusted with a positive correction term χ:

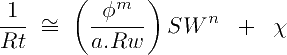
Deep conductivity correction in conductivity to account for clay content


Now this eχtra χ term correction can be modeled as a function χ = χ (Rsh, Vsh, SW). Bardon and Pied (1969) considered that χ should increase proportionately with shale conductivity (1/Rsh) and the volume of shale (VSH). So they proposed: χ ≈ Vsh . SW . (1/Rsh). This conduces to the modified Simandoux equation in terms of conductivity:

The modified Simandoux equation in term of conductivity



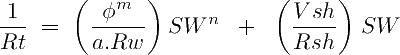
The Simandoux equation is usually the default option to work with shaly rocks. However, many clastic reservoirs with "fresh" salinities of less than 20,000 PPM equiv. NaCl behave better with the Indonesia equation.


As a general rule, we recommend to consider the use of the Indonesia equation for reservoirs with fresh formation waters, the Simandoux equation for salty reservoirs, and to explore the Fertl equation around α=0.30 if Rsh can not be determined because a pure nearby shale body can not be found in the reservoir.


Closed Equation variations for the modified Simandoux model


There are many ways to modify the regular Simandoux equation to become with closed, non-iterative approximations that work well for most of the cases. We show here two fundamental variations: The first variation takes the regular Simandoux equation and avoids iterations by using a custom exponent (2/n), in same style as the Indonesia equation:


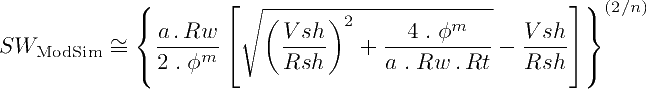
First variation of the Modified Simandox Equation


The second variation not only uses the Bardon and Pied (1969) χ conductivity term and the custom exponent (2/n). It also applies an inflation factor 1/(1-Vsh) to the Archie conductivity term:


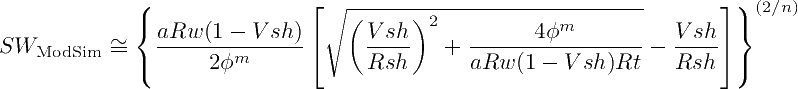
Second variation of the Modified Simandox Equation



Take Notes Related articles:

© 2012-2023 GeolOil LLC. Please link or refer us under Creative Commons License CC-by-ND