GeolOil - How to calculate fracture porosity from well logs

Fracture porosity is the ratio between the volume of open fractures and the rock's bulk volume. The fracture porosity, if present, is one of the contributions to the rock's porosity. The other porosity contributions are other sources of secondary porosity like vugs or vugular porosity, effective matrix porosity, and non effective matrix porosity like clay cement porosity.

Secondary porosity is classically estimated from well logs as the difference of total density porosity minus total sonic porosity φ_f ≅ φ_d - φ_s. It is applicable to either carbonate rocks or clastic sandstones that may or may not contain clays. The porosity difference should be similar to that of effective density porosity minus the effective sonic porosity. If the only source of secondary porosity are fractures, then the porosity difference could be a good estimator of the fracture porosity.

Since the sonic speed is higher for the solid rock's fabric or matrix (it's denser than fluid filled pores and fracture gaps), the compressive sonic pulse or wave is mostly transmitted through the matrix. However, the bulk density log and its derived density porosity curve, measures all the porosity spaces. That's why the difference φ_d - φ_s is an estimator to the secondary porosity and fracture porosity. If the rock is shaly and the effective density porosity is not available, it can be replaced by the effective neutron porosity log, but only after it is converted to the correct matrix mineral blend.

$Density porosity minus sonic porosity estimates fracture porosity$

Density - sonic porosity estimates fracture porosity: (brown + blue pore volume) - (brown pore volume) = blue pore volume

Fracture porosity estimation from the density porosity - sonic porosity difference φ_d - φ_s requires good quality logs, knowledge of the rock's minerals, and some properties. The figure below shows the GeolOil Porosity Functions panel equations for:

Density porosity
Wyllie sonic porosity
Raymer sonic porosity
Modified Raymer sonic porosity
Effective Porosity
Secondary Porosity (Fracture porosity if there are no vugs)

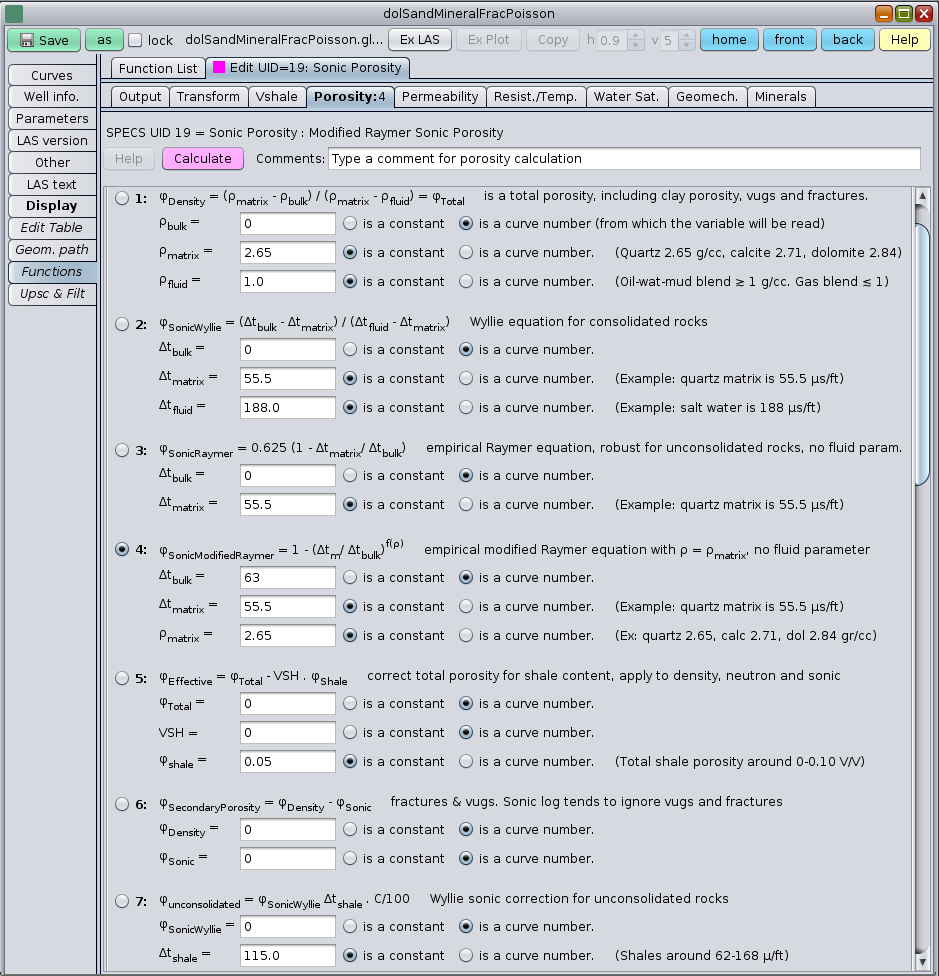
Porosity panel equations for density porosity, Wyllie sonic porosity, Raymer sonic porosity, Modified Raymer sonic porosity, effective porosity, secondary porosity, and porosity for unconsolidated rocks

The figure below shows the GeolOil porosity functions panel.

The Wyllie sonic porosity equation is one of most well known models to estimate sonic porosity. However, it depends upon the sonic travel time of pore fluid, which may be unknown if the fluid column is variable, or if there is a transition zone with a blend of fluids. The modified Raymer sonic porosity removes the fluid dependency and could behave as a robust estimator.

The most critical parameter to calculate sonic porosity is perhaps the matrix compressional travel time Δt_matrix. It is not only usually unknown, but in many reservoirs is not a constant parameter, but a curve that depends on the variable column lithology, its matrix fabric, and rock's stiffness. Since typical values of fracture porosity barely range 0%-4%, its computation may be unstable, requiring good quality curves, and precise parameters.

The following methodology provides some guidance to achieve a reasonable estimation of fracture porosity from logs:

Calculate a first draft of fracture porosity as the algebraic difference φ_d - φ_s without trimming or discarding any negative estimates.

Name this difference curve itself as Quality indicator curve Q(md)

If Q(md) yields too big negative values, or too big positive values, the fracture porosity estimation is completely unreliable and should be discarded at least for the problematic depths.

If Q(md) absolute value magnitude is not so big, try to shift it to the right to remove most of the negative estimates by slightly tunning the matrix compressional travel time Δt_matrix

Finally, replace all negative values with 0 (no fractures at such depths), and trim values exceeding 4% to 4%. Make sure only few depths exceeds 4%, otherwise discard the fracture porosity estimation as it looks unreliable large.

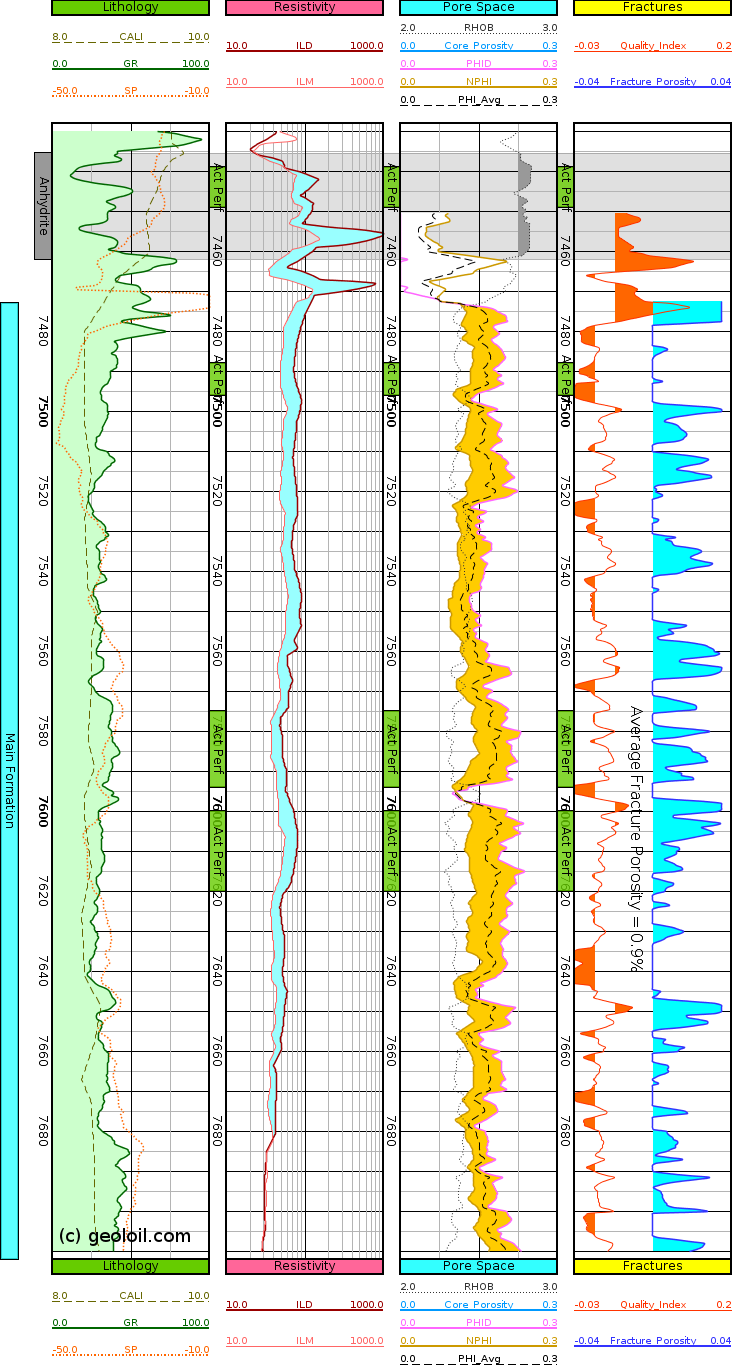
Fracture Porosity estimation log with quality index indicator

Estimation of fracture porosity with a quality index curve for a gas reservoir

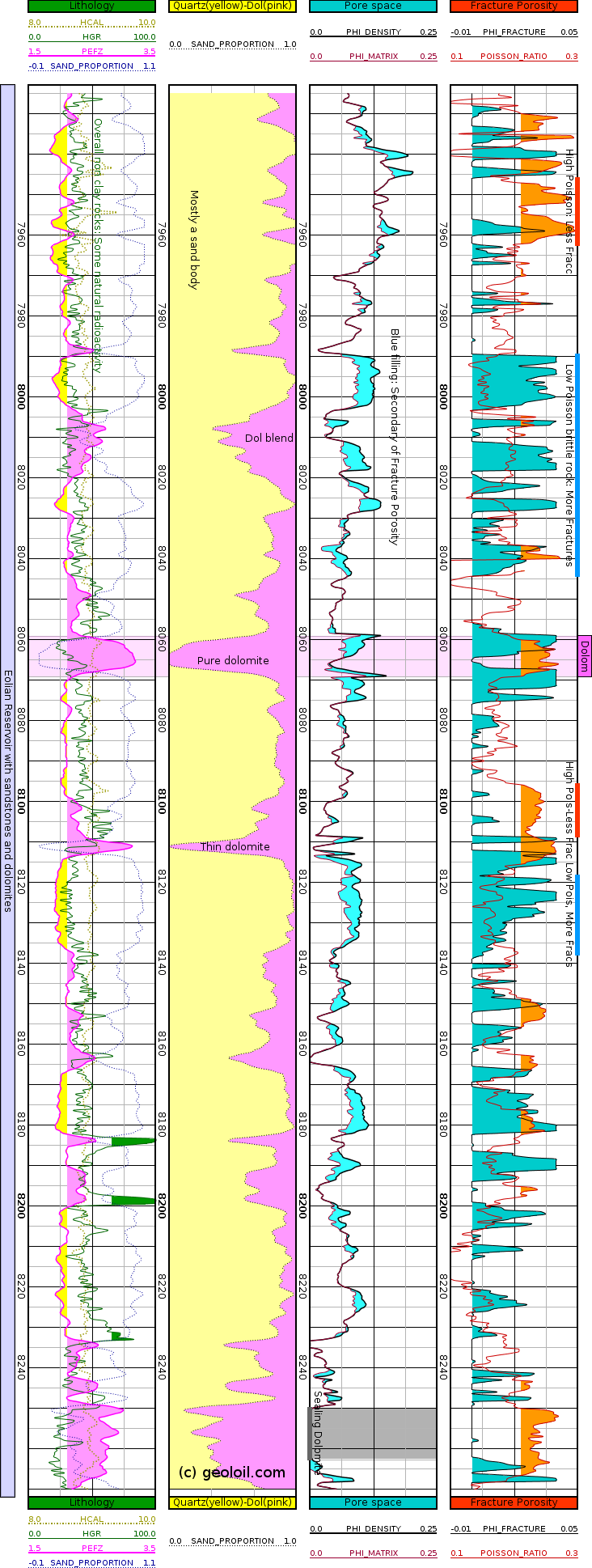
$Relationship between Poisson's ratio ν and fracture porosity$

Another estimation of fracture porosity: the more plastic the rock, less fractures

⚠ NOTE: The techniques presented in this article can only estimate fractures at the log resolution scale —that is, fractures that may be enclosed in the log scale of around few feet—. Any fractures out of this volume would be overlooked, given the false impression that the reservoir has no fractures. ∎

GeolOil is listed by the official SPWLA software directory

Since 2012

GeolOil - How to calculate fracture porosity from well logs