
|
 Downloads
Downloads
|
 Prices
Prices
|
 Videos
Videos
|
GeolOil - How to build permeability correlations from core and well log data
Absolute permeability is one of the most difficult petrophysical properties to model from well log data. The essential problem is that permeability is related to pore throat size rather than the volumetric proportion of connected void space in the rock (effective porosity). So rocks with a same porosity can perfectly have different values of permeability. To add more complexity to the problem, permeability is usually a very heterogeneous property that easily spans over three or even five orders of magnitude in many typical reservoirs.
While porosity can be estimated from regular well log curves, like bulk density and neutron porosity, a log permeability estimate (at curve resolution size) would require curves from NMR Nuclear Magnetic Resonance tools. Since there is a general weak trend that high porosities also show larger pore sizes, correlations are built for permeability as empirical functions of porosity for each rock type k ≅ f(φ). Then, the function f(φ) is applied to the continuous porosity log curve, and a continuous permeability curve is produced for the well.
Core lab measurements that collect paired values of porosity and maximum horizontal permeability (x=φ, y=KhMax) are cross-plotted and the empirical correlation f(φ) is adjusted to the dispersed points. Even after carefully splitting the core samples into several rock types and remove unreliable and influential outliers, adjusted r2 determination coefficients are typically low, around 15% to only 65%.
There are many reasons for these weak correlations:
- As was already said, permeability is related to the pore throat size itself, rather than the porosity
- Permeability depends not only on the scale sample size, but also on the throat geometry path (called tortuosity) along the connected pores through a flow direction. —Indeed, the permeability is a tensor —
- The lab core porosity, if measured with helium, is closer to the total porosity than the effective porosity expected for a sound permeability correlation, because helium may enter into the tiny clay pore spaces.
- The core sample brought from the reservoir to the lab has suffered geo-mechanical stress relaxations and pore throat expansions. Even if the core is put back in a pressurized cell, there might be induced micro fracture openings and closings that randomly alter the permeability, adding noise.
- The plug sample cleaned with toluene may alter the rock and its wetability. Also the plug drying process may alter the clay fabric in the rock.
When fitting empirical f(φ) correlations as univariate functions of the porosity φ, the following functional form, has historically yielded reasonable results:
k = b0 . φb1
The form is converted into a linear expression y=c0+c1x on x and y by taking natural logarithms:
ln(k) = c0 + c1.ln(φ) where: y=ln(k) c0=ln(b0) c1 =b1 and x=ln(φ)
A set of i=1,2,..,n core lab sample measurements of porosity and permeability {(φi, ki)} is then converted to a set of {(xi, yi)} points and then the parameters c0 and c1 can be estimated with techniques like ordinary least squares regression. However, since both x and y are random variables suffering lab errors, —least squares assumption works when y is a random variable, but x is not— a more correct solution is found using Deming orthogonal regression. Its probabilistic solution is:
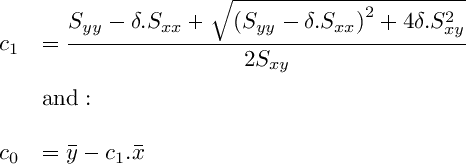
Where:
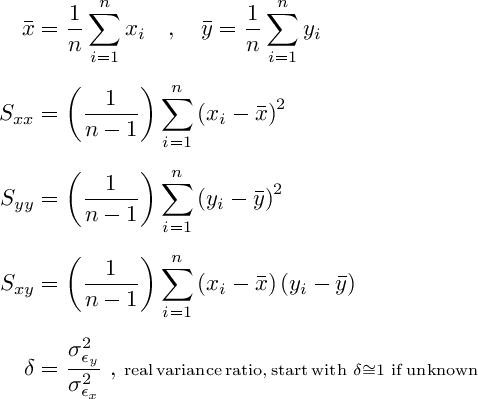
⚠ NOTE:
The use of the correct orthogonal regression solution shown above is important:
If the regular OLS Ordinary Least Squares solution is taking instead,
the slope parameter c1 would be smaller or flatter than it should be
(specially if the determination coefficient r2 is quite small). So OLS will fail to reproduce most
of the permeability range, and in extreme cases, the estimated permeability would be almost a constant value.
∎
Beyond the one to one univariate porosity-permeability simple correlation discussed, there is no reason why other regressor variables can't be added to enrich and increase the adjusted determination coefficient r2. The figure below shows the GeolOil work-flow panel with some built-in permeability correlations from core data.
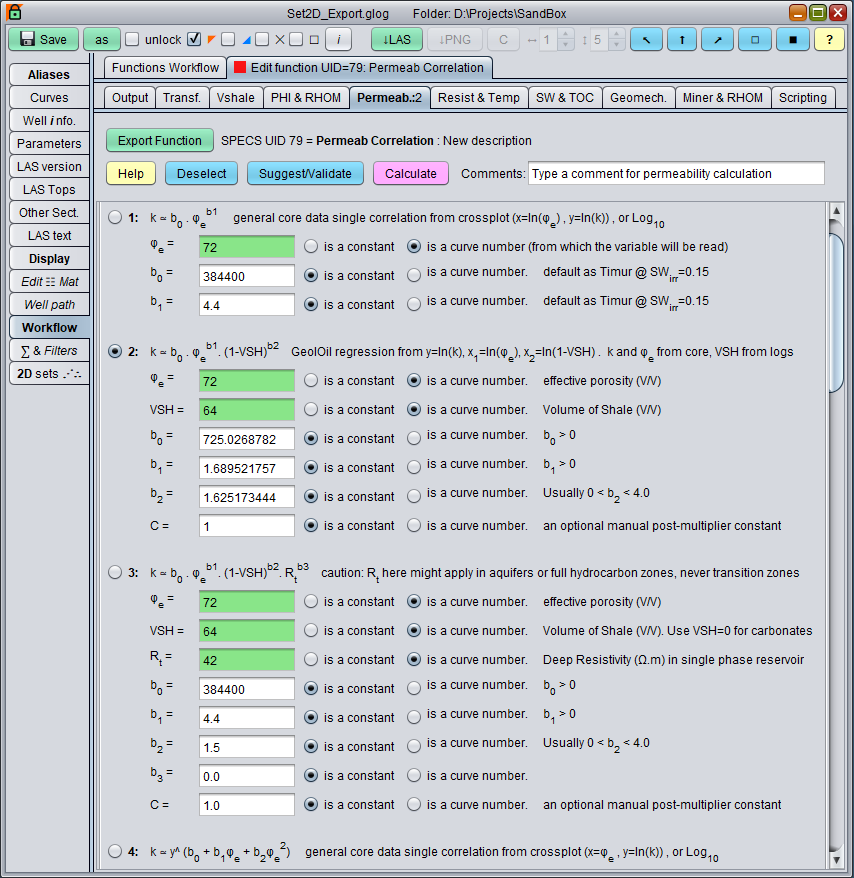
The GeolOil software panel with major built-in permeability correlations from core data
A particularly interesting equation is the second one in the above panel. It establishes a multiple regression of permeability as a join function with both porosity and volume of shale VSH: k = b0 . φb1 . (1-VSH)b2
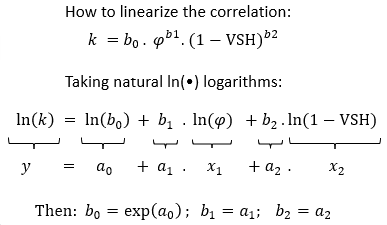
The linearized equation (in the coefficients a0, a1, and a2), can be applied on clastic reservoirs from easily accessible conventional data: permeability and porosity from core laboratory measurements, but VSH shaliness estimated from well log curves (like a Vshale estimated from gamma ray, or from neutron to density porosity difference). In most of the cases, the inclusion of the VSH term, slightly but steadily increases the adjusted determination coefficient, improving the permeability range response compared with a flatter behaviour of a porosity only term equation. The effects of the porosity and shaliness terms on permeability can be interpreted as follows:
- If porosity increases, permeability increases. This is because there is a trend that higher porosities show larger pore throats, and hence bigger permeabilities.
- If shaliness VSH increases (1-VSH decreases), the permeability decreases. Perhaps a slow depositional environment with clays might be related with smaller grains and smaller pore throats, hence smaller permeabilities. Also don't worry too much about multi-collinearity collisions between effective porosity and Vshale, because their correlation is weak.
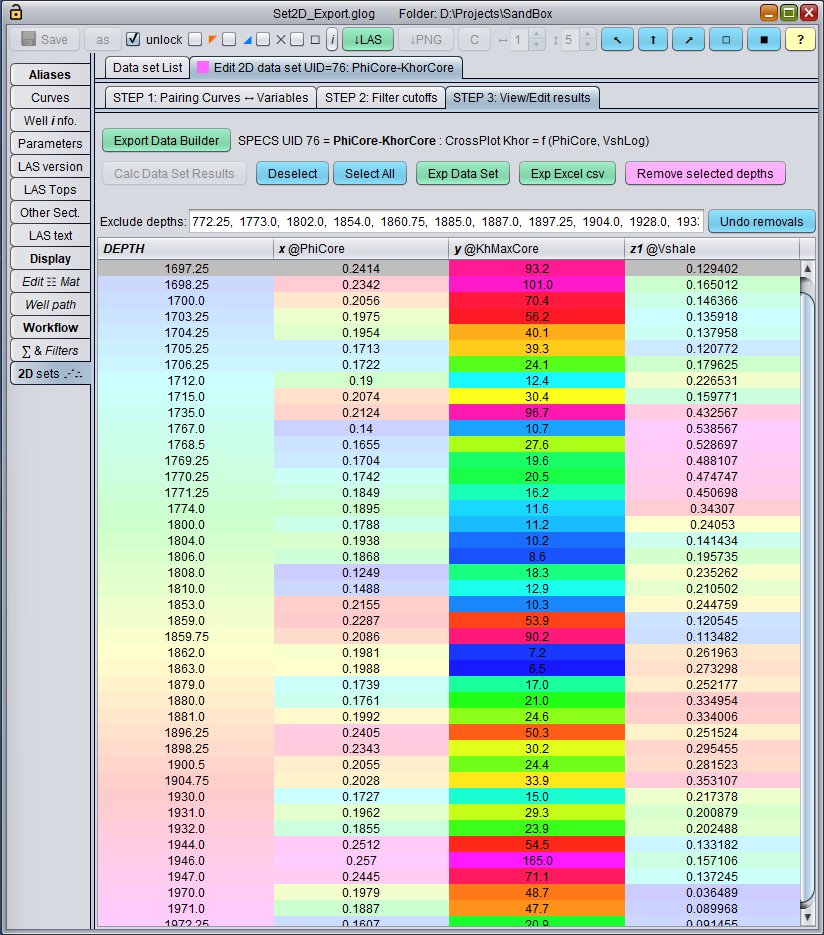
The GeolOil core data selection panel to export results to an Excel spreadsheet
The above panel shows the expected general relationships discussed for core data from a clastic reservoir. The maximum horizontal permeability KhMaxCore is highlighted with saturated colors at the center column. Comparing the with the left PhiCore column, it can be seen matching color behaviours: warm red tones like reds in permeability are paired with warm red tones in porosity, and blue tones with blues and greens. Likewise, an inverse color relationship is observed with the right column Vshale, permeability warm colors like reds are paired with blues and green colors, and vice versa.

Well log plot from a clastic reservoir with permeability and porosity core data
The corresponding well log plot is shown in the image above. Although the curves and core data quality are not the best, it displays other interesting features. The permeability track shows the core data points together with the continuous black curve of absolute permeability computed from the fitted equation k = b0 . φb1 . (1-VSH)b2 and also the permeabilities KO and KW to Oil (green) and Water (blue) respectively. Notice a good match behaviour of KW with the free movable water estimate (the difference between SWe and SWirr curves) at the right most saturations track (the blue filling).
The next figure shows the fitted permeability equation computed with Excel after exporting the CSV data. Although the overall r2 fit value is low, it shows the expected behaviour. Notice also that all the green regression P-values are highly significant (less than 1%), so the terms Phi and VSH legit-amiable enter into the model with valid statistical contributions.

Fitted model of permeability versus porosity and Vshale

|
Related article:
|

|
Related video:
|
 GeolOil is listed by the official
SPWLA software directory
GeolOil is listed by the official
SPWLA software directory
| |



|
|
|
© 2012-2026 GeolOil LLC. Please link or refer us under Creative Commons License CC-by-ND |




 TRAINING
TRAINING

 PAPERS
PAPERS
 REFERENCES
REFERENCES
 GET IN TOUCH
GET IN TOUCH

