
|
 Downloads
Downloads
|
 Prices
Prices
|
 Videos
Videos
|
|
"I love Petrophysics" |
GeolOil - How to estimate Porosity from Flushed-Zone Rxo invaded Resistivity
By: Oscar Gonzalez, GeolOil LLC. This paper was first published on April 2020 on geoloil.com
Porosity can be estimated from the log curve of flushed zone resistivity Rxo. Since the drilling mud invades the zone closest to the borehole wall, it displaces most of the hydrocarbons, so the local hydrocarbon saturation in such small zone can drop easily to around 20% or less.
The Archie equation can be applied then to this invaded zone —for now let's assume that the rock matrix is clean, non-clayey, and non conductive—. Replacing the deep, true far field uninvaded resistivity Rt with the flushed zone resistivity Rxo, and replacing the formation water resistivity Rw with the mud filtrate resistivity Rmf (which has to be corrected to the depth temperature), and solving for the porosity φ:
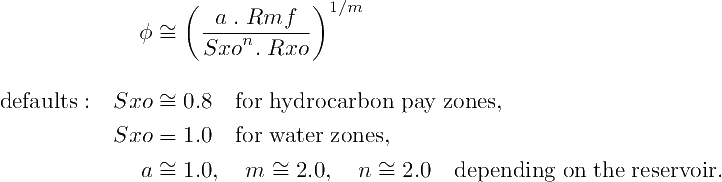
The former equation is appealing. Provided that a good quality curve for Rxo is available in a good quality and stable borehole —occasionally MSFL yields good results—, and Rmf is accurately measured and converted to the depth temperature, the estimator for porosity is useful. This φ estimate is independent of the classics density porosity, neutron porosity, and sonic porosity. It is based only on resistivity and provides yet another in situ estimate, valuable either for validation or even estimation on its own right.
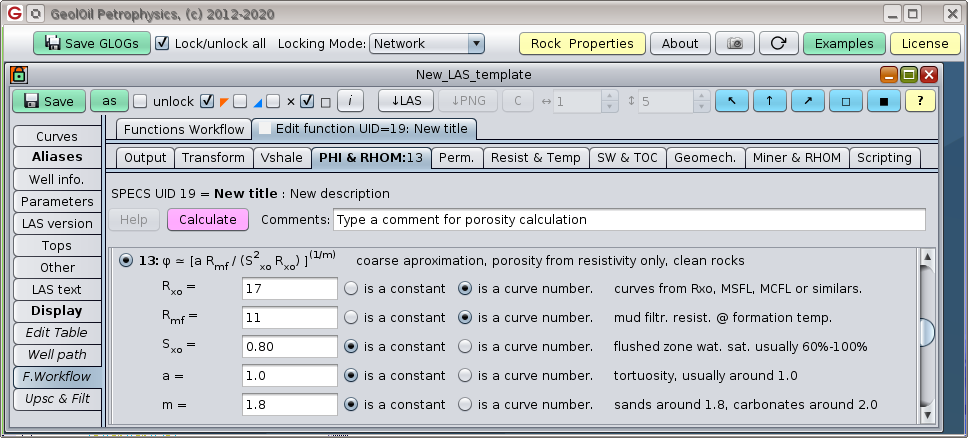
The GeolOil Panel to estimate porosity on clean reservoirs from Rxo
How can we deal with clayey matrices with excess of conductivity? Certainly the Archie equation is not suitable for such cases. In this article —first published in this geoloil.com web-page on April 2020— we introduce a correction to deal with shaly reservoirs. Just take the Indonesia equation for water saturation. After following the same algebraic steps, an approximation to estimate the effective porosity φe with a correction for shale content is:
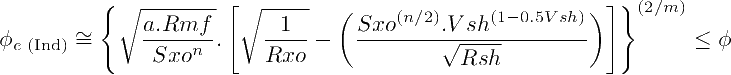
The former equation provides a correction for shale content, and may work for moderately shaly rocks (say VSH ≤ 30%). However, it requires knowledge of an additional parameter, the shale resistivity Rsh. If a nearby pure shale can not be found around the study zone —and also we must assume that such shale has a similar nature than the dispersed shales inside the target rock—, the formula is of little use.
One workaround is the use instead the Fertl equation for water saturation as a coarse approximation (it does not depend on Rsh). After following the same algebraic steps, it is found:
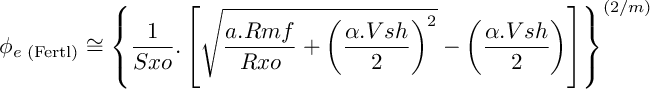
Both former equations can be blended into a unique estimate. Use w=1 if Rshale can be estimated with reasonable accuracy. Use w=0 if Rshale is not reliable at all, and use intermediate values around w=0.5 for a general, more robust estimate under uncertainty:
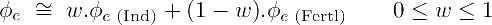
⚠
REMARKS:
The techniques described require good quality data and a stable borehole to work, otherwise the results may be misleading:
![]() One robust feature of the estimated in-situ micro-resistivity porosity,
is that its value is independent of the fluids nature
in the pore space —it only uses resistivity data—.
This is specially useful when working with gas reservoirs, for which carefully adjustments
have to be made to neutron porosity and density porosity to avoid porosity under-estimation and over-estimation.
One robust feature of the estimated in-situ micro-resistivity porosity,
is that its value is independent of the fluids nature
in the pore space —it only uses resistivity data—.
This is specially useful when working with gas reservoirs, for which carefully adjustments
have to be made to neutron porosity and density porosity to avoid porosity under-estimation and over-estimation.
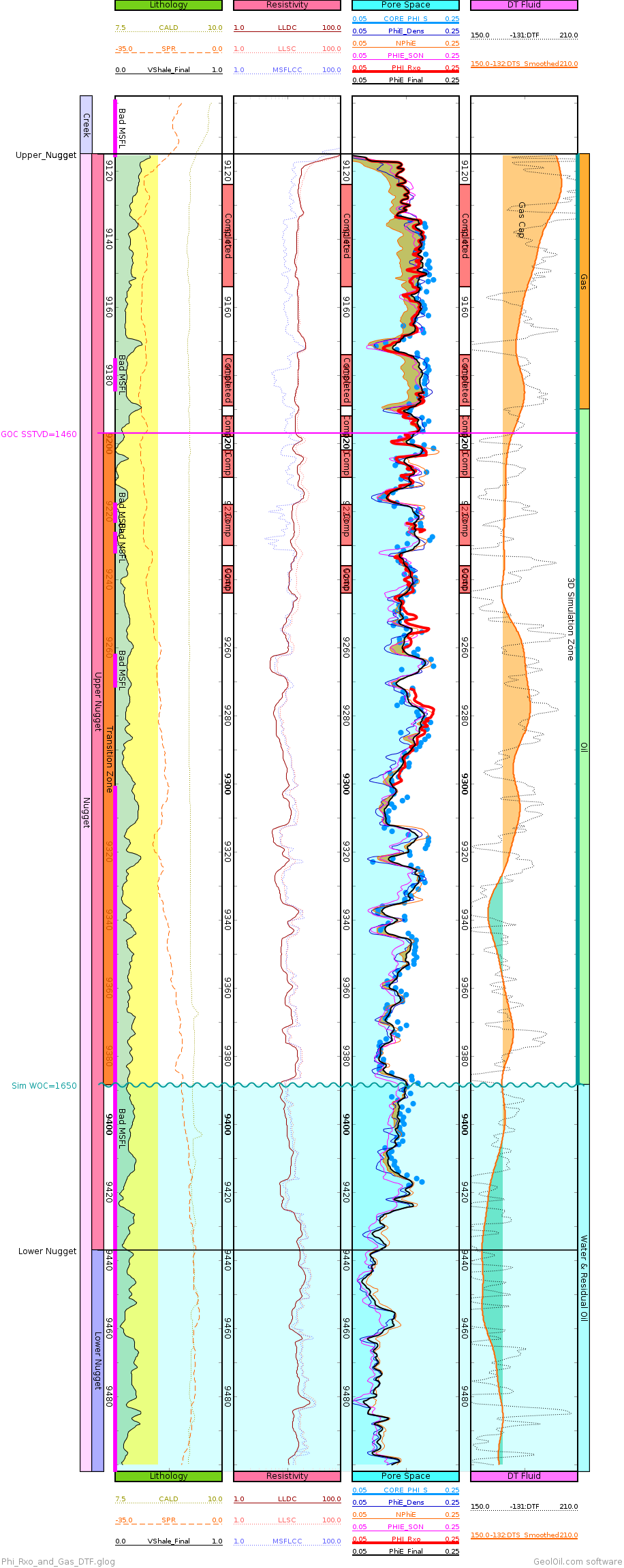
Comparisons of porosities from core, density, neutron porosity, sonic, and micro-resistivity porosity
✔ NOTE: The GLOG file work-flow for this log is available for download with the set of optional interpretation examples.
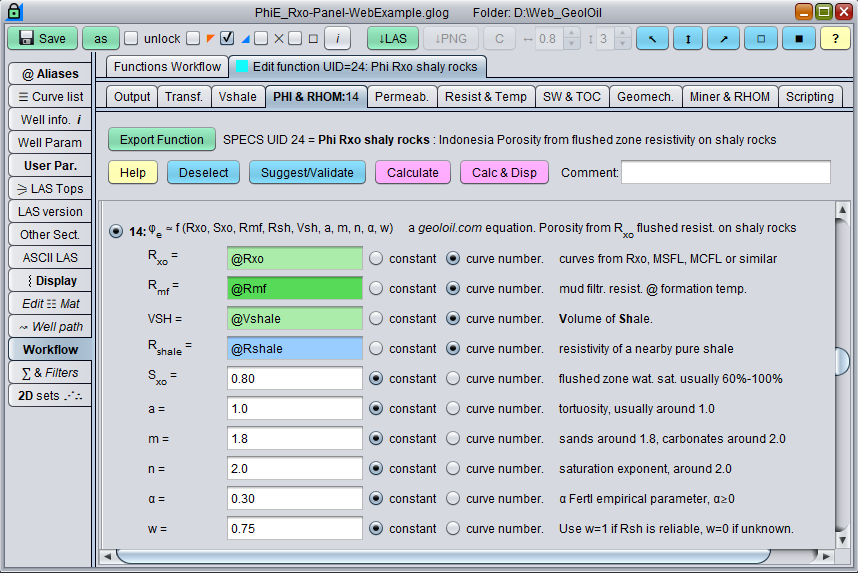
Computation panel to estimate porosity for flushed zone, invaded Rxo resistivity in shaly sands

|
Related articles:
|
 GeolOil is listed by the official
SPWLA software directory
GeolOil is listed by the official
SPWLA software directory
| |



|
|
|
© 2012-2026 GeolOil LLC. Please link or refer us under Creative Commons License CC-by-ND |




 TRAINING
TRAINING

 PAPERS
PAPERS
 REFERENCES
REFERENCES
 GET IN TOUCH
GET IN TOUCH

